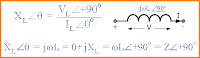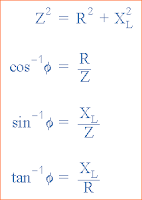Induktansi AC dan Reaktansi Induktif

Oposisi atau perlawanan terhadap aliran arus melalui Induktor bolak-balik (AC) disebut Reaktansi Induktif dan yang secara linier tergantung pada frekuensi pasokan (supply). Induktor dan choke pada dasarnya adalah gulungan atau lilitan kawat yang dililitkan di sekitar tabung bekas berongga (berinti udara) atau wound arround beberapa bahan feromagnetik (berinti besi) untuk meningkatkan nilai induktif yang disebut induktansi.

Induktor menyimpan energi mereka dalam bentuk medan magnet yang dibuat ketika tegangan diterapkan di terminal induktor. Pertumbuhan arus yang mengalir melalui induktor tidak instan tetapi ditentukan oleh induktor sendiri yang diinduksi sendiri atau nilai ggl balik.

Kemudian untuk kumparan induktor, ini ggl balik tegangan VL sebanding dengan laju perubahan arus yang mengalir melalui itu. Arus ini akan terus naik sampai mencapai kondisi stabil maksimumnya yaitu sekitar lima konstanta waktu ketika ggl balik yang diinduksi sendiri ini telah meluruh ke nol.

Pada titik ini arus tunak (steady state) mengalir melalui coil, tidak ada ggl balik yang diinduksi untuk menentang aliran arus dan oleh karena itu, kumparan bertindak lebih seperti konsleting yang memungkinkan arus maksimum mengalir melewatinya. Namun, dalam rangkaian arus bolak-balik yang berisi Induktansi AC, aliran arus melalui induktor berperilaku sangat berbeda dengan tegangan DC keadaan tunak.

Sekarang di rangkaian AC, perlawanan terhadap arus yang mengalir melalui belitan tidak hanya tergantung pada induktansi kumparan tetapi juga frekuensi dari bentuk gelombang tegangan yang diterapkan karena bervariasi dari nilai positif ke negatif.

Resistansi aktual terhadap arus yang mengalir melalui Coil dalam rangkaian AC ditentukan oleh Resistansi AC coil dengan resistansi AC ini diwakili oleh bilangan kompleks. Tetapi untuk membedakan nilai resistansi DC dari nilai resistansi AC, yang juga dikenal sebagai Impedansi, istilah Reaktansi digunakan.

Seperti resistansi, reaktansi diukur dalam Ohm tetapi diberi simbol "X" untuk membedakannya dari nilai "R" murni resistif dan karena komponen yang dimaksud adalah induktor, reaktansi induktor disebut Reaktansi Induktif, ( XL ) dan diukur dalam Ohm. Nilainya dapat ditemukan dari rumus.

Reaktansi Induktif

XL = 2πƒL

Di mana: XL adalah Reaktansi Induktif dalam Ohm, ƒ adalah frekuensi dalam Hertz dan L adalah induktansi dari coil di Henries. Kita juga dapat mendefinisikan reaktansi induktif dalam radian, di mana Omega, ω sama dengan 2πƒ

XL = ωL

Jadi setiap kali tegangan sinusoidal diterapkan pada kumparan induktif, ggl balik menentang naik turunnya arus yang mengalir melalui kumparan dan dalam kumparan induktif murni yang tidak memiliki resistansi atau kerugian nol, impedansi ini (yang bisa berupa bilangan kompleks) sama dengan reaktansi induktifnya. Reaktansi juga diwakili oleh vektor karena memiliki besaran dan arah (sudut). Pertimbangkan rangkaian di bawah ini.

Induktansi AC dengan Supply Sinusoidal

Rangkaian sederhana di atas terdiri dari induktansi murni L Henries ( H ), yang terhubung melintasi tegangan sinusoidal yang diberikan oleh ekspresi: V(t) = Vmax sin ωt.

Ketika sakelar ditutup tegangan sinusoidal ini akan menyebabkan arus mengalir dan naik dari nol ke nilai maksimum. Kenaikan atau perubahan arus ini akan menyebabkan medan magnet di dalam coil yang pada gilirannya akan menentang atau membatasi perubahan arus ini.

Tetapi sebelum arus memiliki waktu untuk mencapai nilai maksimum seperti pada rangkaian DC, tegangan berubah polaritas menyebabkan arus berubah arah. Perubahan ke arah lain ini sekali lagi ditunda oleh ggl-balik induksi-sendiri kembali coil, dan dalam rangkaian yang mengandung induktansi murni saja, saat ini tertunda oleh 90°.

Tegangan yang diterapkan mencapai nilai positif maksimumnya seperempat ( 1/4ƒ ) dari siklus lebih awal dari arus mencapai nilai positif maksimumnya, dengan kata lain, tegangan yang diterapkan ke sirkuit induktif murni "LEADS/memimpin" arus dengan seperempat dari siklus atau 90° seperti yang ditunjukkan di bawah ini.

Bentuk Gelombang Sinusoidal untuk Induktansi AC

Efek ini juga dapat diwakili oleh diagram fasor berada di rangkaian murni induktif tegangan “MEMIMPIN” arus sebesar 90°. Tapi dengan menggunakan tegangan sebagai referensi kami, kami juga dapat mengatakan bahwa arus “TERTINGGAL” oleh tegangan seperempat dari sebuah siklus atau 90° seperti yang ditunjukkan dalam diagram vektor di bawah ini.

Diagram Fasor untuk Induktansi AC

Jadi untuk kerugian murni kurang induktor, VL "NAIK" IL sebesar 90°, atau kita dapat mengatakan bahwa IL "turun" VL oleh 90°.

Ada banyak cara yang berbeda untuk mengingat hubungan fasa antara tegangan dan arus yang mengalir melalui rangkaian induktor murni, tetapi satu cara yang sangat sederhana dan mudah diingat adalah dengan menggunakan ungkapan mnemonik "ELI" (diucapkan Ellie seperti dalam nama perempuan).

ELI adalah singkatan dari E lectromotive force terlebih dahulu dalam induktansi AC, L sebelum arus I. Dengan kata lain, tegangan sebelum arus dalam induktor, E , L , I sama dengan "ELI" , dan di mana pun fasa-fasa tegangan dimulai, ungkapan ini selalu berlaku untuk rangkaian induktor murni.

Pengaruh Frekuensi pada Reaktansi Induktif

Ketika supply 50Hz dihubungkan dengan sebuah cocok Induktansi AC, arus akan tertunda oleh 90° seperti yang dijelaskan sebelumnya dan akan mendapatkan nilai puncak I amp sebelum tegangan berbalik polaritas pada akhir setiap setengah siklus, yaitu saat naik ke atas ke nilai maksimum dalam " T detik ".

Jika sekarang kita menerapkan supply 100Hz dari tegangan puncak yang sama ke coil, arus masih akan tertunda hingga 90° tetapi nilai maksimumnya akan lebih rendah dari nilai 50Hz karena waktu yang dibutuhkan untuk mencapai nilai maksimumnya telah berkurang karena dengan peningkatan frekuensi karena sekarang hanya memiliki " 1/2 T detik " untuk mencapai nilai puncaknya. Selain itu, laju perubahan fluks dalam coil juga meningkat karena peningkatan frekuensi.

Kemudian dari persamaan di atas untuk reaktansi induktif, dapat dilihat bahwa jika Frekuensi ATAU Induktansi ditingkatkan, nilai reaktansi induktif keseluruhan coil juga akan meningkat. Ketika frekuensi meningkat dan mendekati tak terhingga, reaktansi induktor dan karenanya impedansinya juga akan meningkat menuju tak terhingga yang bertindak seperti rangkaian terbuka.

Demikian juga, ketika frekuensi mendekati nol atau DC, reaktansi induktor juga akan berkurang menjadi nol, bertindak seperti konsleting. Ini berarti bahwa reaktansi induktif adalah "berbanding lurus dengan frekuensi" dan memiliki nilai kecil pada frekuensi rendah dan nilai tinggi pada frekuensi lebih tinggi seperti yang ditunjukkan.

Reaktansi Induktif Terhadap Frekuensi

Reaktansi induktif dari sebuah induktor meningkat dengan meningkatnya frekuensi di atasnya karena itu reaktansi induktif sebanding dengan frekuensi (XL α ƒ) karena ggl-balik yang dihasilkan dalam induktor sama dengan induktansinya dikalikan dengan laju perubahan arus dalam induktor. Juga saat frekuensi meningkat, arus yang mengalir melalui induktor juga mengurangi nilainya.

Kami dapat menyajikan efek frekuensi yang sangat rendah dan sangat tinggi pada reaktansi Induktansi AC murni sebagai berikut:

Dalam rangkaian AC yang mengandung induktansi murni, rumus berikut ini berlaku:

Jadi bagaimana kita sampai pada persamaan ini. Nah ggl yang diinduksi sendiri dalam induktor ditentukan oleh Hukum Faraday yang menghasilkan efek induksi-diri pada induktor karena laju perubahan arus dan nilai maksimum ggl yang diinduksi akan sesuai dengan laju perubahan maksimum. Kemudian tegangan dalam coil induktor diberikan sebagai:

maka tegangan melintasi induktansi AC akan didefinisikan sebagai:

VL = ωL Imax sin (ωt+90°)

Dimana: VL  = IωL yang merupakan amplitudo tegangan dan θ = + 90° yang merupakan perbedaan fasa atau sudut fasa antara tegangan dan arus.

Pada Domain Fasor

Dalam domain fasor tegangan melintasi kumparan diberikan sebagai:

VL = jωLI

dimana:

jωL = jXL = 2πfL = IMPEDANSI, Z

dan dalam Bentuk Polar/Kutub ini akan ditulis sebagai:   X L ∠90° di mana:

AC melalui Rangkaian Seri R + L

Kita telah melihat di atas bahwa arus yang mengalir melalui kumparan induktif murni meninggalkan tegangan sebesar 90° dan ketika kita mengatakan kumparan induktif murni, yang kita maksudkan adalah kumparan induktif yang tidak memiliki hambatan ohmik dan oleh karena itu, tanpa I2R rugi. Tetapi kenyataanya, tidak mungkin memiliki Induktansi AC murni saja.

Semua kumparan listrik, relai, solenoid, dan trafo/transformator akan memiliki sejumlah resistansi, sekecil apa pun yang terkait dengan belitan kawat yang digunakan. Ini karena kawat tembaga memiliki resistivitas.

Kemudian kita dapat menganggap kumparan induktif kita sebagai kumparan induktif yang memiliki resistansi, seri R dengan induktansi, L yang menghasilkan apa yang secara umum disebut "induktansi tidak murni".

Jika coil memiliki beberapa resistansi "internal" maka kita perlu mewakili total impedansi coil sebagai resistansi secara seri dengan induktansi dan dalam rangkaian AC yang berisi induktansi, L dan resistansi, R tegangan, V di seluruh kombinasi akan menjadi jumlah fasor dari dua tegangan komponen, VR dan VL .

Ini berarti kemudian bahwa arus yang mengalir melalui kumparan masih akan tertinggal tegangan, tetapi dengan jumlah kurang dari 90° tergantung pada nilai-nilai VR dan VL, jumlah fasor. Sudut baru antara tegangan dan bentuk gelombang saat ini memberi kita perbedaan fasa yang seperti kita ketahui adalah sudut fasa rangkaian yang diberi simbol Yunani phi, Φ .

Pertimbangkan rangkaian di bawah ini adalah resistansi non-induktif murni, R dihubungkan secara seri dengan induktansi murni, L.

Resistansi Seri - Rangkaian Induktansi

Dalam rangkaian RL seri di atas, kita dapat melihat bahwa arus adalah umum untuk kedua resistansi/perlawanan dan induktansi sementara tegangan terdiri dari dua tegangan komponen, VR dan VL. Tegangan yang dihasilkan dari kedua komponen ini dapat ditemukan secara matematis atau dengan menggambar diagram vektor.

Untuk dapat menghasilkan diagram vektor, referensi atau komponen umum harus ditemukan dan dalam rangkaian AC seri, arus adalah sumber referensi karena arus yang sama mengalir melalui resistansi dan induktansi. Diagram vektor individu untuk resistansi murni dan induktansi murni diberikan sebagai:

Diagram Vektor untuk Dua Komponen Murni

Kita dapat melihat dari atas dan dari tutorial sebelumnya tentang Resistansi AC bahwa tegangan dan arus dalam rangkaian resistif sama-sama dalam fasa dan oleh karena itu vektor VR ditarik dengan cara ditumpangkan ke skala ke vektor arus.

Juga dari atas diketahui bahwa arus tertinggal tegangan dalam induktansi AC (murni) rangkaian karena itu vektor VL diambil 90° di depan arus dan dengan skala yang sama seperti VR seperti yang ditunjukkan.

Diagram Vektor dari Tegangan yang Dihasilkan

Dari diagram vektor di atas, kita dapat melihat bahwa garis OB adalah referensi arus horizontal dan garis OA adalah tegangan yang melintasi komponen resistif yang selaras dengan arus. Baris OC menunjukkan tegangan induktif yang 90° di depan arus oleh karena itu masih bisa dilihat bahwa arus tertinggal tegangan murni induktif sebesar 90°. Jalur OD memberi kita tegangan supply yang dihasilkan. Kemudian:

V sama dengan nilai rms dari tegangan yang diberikan.

I sama dengan nilai rms dari arus seri.

VR sama dengan penurunan tegangan I.R pada resistansi yang berada dalam fase dengan arus.

VL sama dengan I.XR jatuh tegangan induktansi yang mengarah saat ini sebesar 90°.

Seperti arus tertinggal tegangan dalam induktansi murni dengan persis 90° resultan fasor diagram diambil dari tegangan turun individu VR dan VL merupakan segitiga tegangan siku kanan yang ditunjukkan di atas sebagai OAD.

Kemudian kita juga dapat menggunakan teorema Pythagoras untuk secara matematis menemukan nilai tegangan yang dihasilkan ini di rangkaian Resistor / Induktor (RL).

Seperti VR  = I.R dan VL  = I.XL tegangan yang diberikan akan menjadi jumlah vektor dari dua sebagai berikut:

Kuantitas   mewakili impedansi, Z dari rangkaian.

Impedansi Induktansi AC

Impedansi, Z adalah resistansi/perlawanan "TOTAL" untuk arus yang mengalir dalam rangkaian AC yang berisi Resistansi, (bagian nyata) dan Reaktansi (bagian imajiner). Impedansi juga memiliki unit Ohm, Ω. Impedansi tergantung pada frekuensi, ω dari rangkaian karena hal ini mempengaruhi komponen reaktif rangkaian dan dalam rangkaian seri semua impedansi resistif dan reaktif ditambahkan bersama-sama.

Impedansi juga dapat diwakili oleh bilangan kompleks, Z = R + jXL tetapi bukan fasor, ini adalah hasil dari dua atau lebih fasor yang digabungkan bersama. Jika kita membagi sisi-sisi dari segitiga tegangan di atas dengan I, segitiga lain diperoleh yang sisi-sisinya mewakili resistansi, reaktansi, dan impedansi rangkaian seperti yang ditunjukkan di bawah ini.

Segitiga Impedansi RL

Impedansi dari Induktor AC Segitiga Impedansi

Kemudian: (Impedansi)2 = (Resistansi)2 + (Reaktansi j)2 di mana j mewakili pergeseran fasa 90°. Ini berarti bahwa sudut fase positif, θ antara tegangan dan arus diberikan sebagai.

Sudut Fasa

Sementara contoh kami di atas mewakili induktansi AC non-murni sederhana, jika dua atau lebih kumparan induktif dihubungkan bersama-sama secara seri atau kumparan tunggal dihubungkan secara seri dengan banyak resistansi non-induktif, maka total resistansi untuk elemen resistif akan sama ke: R1 +R2 + R3 dst, memberikan nilai resistif total untuk rangkaian.

Demikian juga, total reaktansi untuk elemen induktif akan sama dengan: X1 + X2 + X3 dst, memberikan nilai total reaktansi untuk rangkaian. Dengan cara ini rangkaian yang mengandung banyak choke, kumparan dan resistor dapat dengan mudah direduksi menjadi nilai impedansi, Z terdiri dari resistansi tunggal dalam seri dengan reaktansi tunggal, Z2 = R2 + X2.

Contoh: Induktansi AC No.1

Dalam rangkaian berikut, tegangan supply didefinisikan sebagai: V(t) = 230 sin (314t - 30°) dan L = 2.2H . Tentukan nilai arus yang mengalir melalui coil dan gambar diagram fasor yang dihasilkan.

Tegangan melintasi kumparan akan sama dengan tegangan supply. Mengubah nilai domain waktu ini ke dalam bentuk kutub memberi kita: VL = 230 ∠-30° (v). Reaktansi induktif kumparan adalah: XL = ωL = 314 x 2.2 = 690Ω. Maka arus yang mengalir melalui coil dapat ditemukan menggunakan hukum Ohm sebagai:

Dengan arus yang tertinggal tegangan sebesar 90° diagram fasor akan.

Contoh: Induktansi AC No.2

Coil memiliki resistansi 30Ω dan induktansi 0,5H. Jika arus yang mengalir melalui coil adalah 4amps. Apa yang akan menjadi nilai tegangan supply jika frekuensinya 50Hz.

Impedansi rangkaian akan:

Kemudian tegangan turun di setiap komponen dihitung sebagai:

VS = I.Z =  4x159.8 = 640v

VR = I.R = 4x30 = 120v

VL = I.XL = 4x157 = 628v

Sudut fase antara tegangan arus dan supply dihitung sebagai:

Diagram fasor akan menjadi.

Dalam tutorial berikutnya tentang Kapasitansi AC kita akan melihat hubungan tegangan-arus Kapasitor ketika bentuk gelombang AC sinusoidal tunak (steady state) diterapkan untuk itu bersama dengan representasi diagram fasor untuk kapasitor murni dan non-murni.