Desain Filter Butterworth dengan Low Pass Butterworth

Dalam aplikasi yang menggunakan filter untuk membentuk spektrum frekuensi dari sinyal seperti dalam sistem komunikasi atau kontrol, bentuk atau lebar roll-off juga disebut "band transisi", karena filter orde-1 pertama yang sederhana mungkin terlalu panjang atau filter lebar dan aktif yang dirancang dengan lebih dari satu "orde" diperlukan. Jenis-jenis filter ini umumnya dikenal sebagai filter "Orde Tinggi" atau "orde ke-n".

Kompleksitas atau jenis filter ditentukan oleh "orde" filter, dan yang bergantung pada jumlah komponen reaktif seperti kapasitor atau induktor dalam desainnya.

Kita juga tahu bahwa laju roll-off dan karenanya lebar pita/band transisi, tergantung pada jumlah orde filter dan bahwa untuk filter orde-1 pertama sederhana memiliki tingkat roll-off standar 20dB/dekade atau 6dB/oktaf.

Kemudian, untuk filter yang memiliki orde nomor ke- n, itu akan memiliki tingkat roll-off berikutnya 20n dB/dekade atau 6n dB/oktaf. Jadi filter orde-1 pertama memiliki tingkat roll-off 20dB/dekade (6dB/oktaf), filter orde-2 kedua memiliki tingkat roll-off 40dB/dekade (12dB/oktaf), dan filter orde-4 keempat memiliki tingkat roll-off 80dB/dekade (24dB/oktaf), dll.

Filter orde tinggi, seperti orde-3 ketiga, keempat, dan kelima biasanya dibentuk dengan menyatukan filter orde-1 pertama dan orde-2 kedua.

Sebagai contoh, dua low pass filter orde-2 kedua dapat dibuat bersama untuk menghasilkan low pass filter orde-4 keempat, dan seterusnya. Meskipun tidak ada batasan untuk orde filter yang dapat dibentuk, karena orde meningkat begitu juga ukuran dan biaya, juga keakuratannya menurun.

Dekade dan Oktaf

Satu komentar terakhir tentang Dekade dan Oktaf. Pada skala frekuensi, Dekade adalah peningkatan sepuluh kali lipat (kalikan dengan 10) atau penurunan sepuluh kali lipat (bagi dengan 10). Misalnya, 2 hingga 20Hz mewakili satu dekade, sedangkan 50 hingga 5000Hz mewakili dua dekade (50 hingga 500Hz dan kemudian 500 hingga 5000Hz).

Sebuah Oktaf adalah dua kali lipat (kalikan dengan 2) atau mengurangi separuh (bagi dengan 2) dari skala frekuensi. Misalnya, 10 hingga 20Hz mewakili satu oktaf, sedangkan 2 hingga 16Hz adalah tiga oktaf (2 hingga 4, 4 hingga 8 dan akhirnya 8 hingga 16Hz) menggandakan frekuensi setiap kali.

Bagaimanapun juga, skala Logaritmik digunakan secara luas dalam domain frekuensi untuk menunjukkan nilai frekuensi ketika bekerja dengan amplifier dan filter sehingga penting untuk memahaminya.

Skala Frekuensi Logaritmik

Karena resistor penentu frekuensi semuanya sama, dan seperti juga kapasitor penentu frekuensi, frekuensi cut-off atau sudut ( ƒC ) untuk filter orde-1 pertama, kedua, ketiga atau bahkan keempat juga harus sama dan ditemukan dengan menggunakan persamaan yang sudah lama kita kenal:

Seperti halnya filter orde-1 pertama dan kedua, high pass filter orde-3 ketiga dan keempat dibentuk hanya dengan mengubah posisi komponen penentu frekuensi (resistor dan kapasitor) dalam low pass filter yang setara.

Filter Orde tinggi dapat dirancang dengan mengikuti prosedur yang kita lihat sebelumnya dalam tutorial Low Pass Filter dan High Pass Filter. Namun, gain keseluruhan filter orde tinggi diperbaiki karena semua komponen penentu frekuensi sama.

Filter Aproksimasi

Sejauh ini kita telah melihat rangkaian filter orde-1 pertama rendah dan tinggi, respon frekuensi dan fasa yang dihasilkannya.

Filter yang ideal akan memberi kita spesifikasi gain band pass dan kedataran maksimum, redaman band stop minimum dan juga band pass yang sangat curam untuk menghentikan roll band (band transisi) dan oleh karena itu jelas bahwa sejumlah besar respon jaringan akan memenuhi persyaratan ini.

Tidak mengherankan kemudian bahwa ada sejumlah "fungsi aproksimasi" dalam desain filter analog linear yang menggunakan pendekatan matematika untuk memperkirakan fungsi transfer terbaik yang kami butuhkan untuk desain filter.

Desain seperti ini dikenal sebagai Elliptical, Butterworth, Chebyshev, Bessel, Cauer serta banyak lagi lainnya. Dari lima fungsi aproksimasi filter analog linear “klasik” ini hanya Filter Butterworth dan terutama desain low pass filter Butterworth yang akan dianggap di sini sebagai fungsi yang paling umum digunakan.

Desain Rangkaian Low Pass Filter Butterworth

Respon frekuensi dari fungsi aproksimasi/perkiraan Filter Butterworth juga sering disebut sebagai respon "maksimum datar" (tanpa riak) karena band pass dirancang untuk memiliki respon frekuensi yang setipis mungkin secara matematis mulai dari 0 Hz (DC) hingga frekuensi cut-off di -3dB tanpa riak.

Frekuensi yang lebih tinggi di luar titik cut-off roll-off ke nol di band berhenti di 20dB/dekade atau 6dB/oktaf. Ini karena ia memiliki "faktor kualitas", "Q" hanya 0,707.

Namun, satu kelemahan utama dari filter Butterworth adalah bahwa hal itu mencapai kerataan band pass ini dengan mengorbankan band transisi yang lebar karena filter berubah dari Band Pass Filter ke Band Stop Filter.

Ini juga memiliki karakteristik fasa yang buruk juga. Respon frekuensi ideal, disebut sebagai dinding bata atau "brick wall"  filter, dan perkiraan Butterworth standar, untuk orde filter yang berbeda diberikan di bawah ini.

Respon Frekuensi Ideal untuk Filter Butterworth

Perhatikan bahwa semakin tinggi orde filter Butterworth, semakin tinggi jumlah tahapan berjenjang yang ada dalam desain filter, dan semakin dekat filter menjadi respon "brick wall" yang ideal.

Namun dalam praktiknya, respon frekuensi Butterworth ideal tidak dapat dicapai karena menghasilkan riak band pass yang berlebihan.

Di mana persamaan umum yang mewakili filter "n" filter Butterworth, respon frekuensi diberikan sebagai:

Di mana: n merepresentasikan orde filter, Omega ω sama dengan 2πƒ dan Epsilon ε adalah gain band maksimum, (Amax). Jika Amax didefinisikan pada frekuensi yang sama dengan cut-off -3dB titik sudut (ƒc), ε kemudian akan sama dengan satu dan karenanya ε2 juga akan menjadi satu.

Namun, jika Anda sekarang ingin mendefinisikan Amax pada nilai gain tegangan yang berbeda, misalnya 1dB, atau 1.1220 (1dB = 20*logAmax ) maka nilai baru epsilon, ε ditemukan oleh:

Dimana:

 H0 = Gain Band Pass Maksimum, Amax.

 H1 = Gain Pass band Minimum.

Alihkan persamaannya menjadi:

Respon Frekuensi dari filter dapat didefinisikan secara matematis oleh nya Fungsi Transfer dengan standar Fungsi Transfer Tegangan H(jω) ditulis sebagai:

 Dimana:

 Vout = tegangan sinyal output.

 Vin  = tegangan sinyal input.

   j  = ke akar kuadrat dari -1 (√-1 )

  ω  = frekuensi radian (2πƒ)

Catatan: (jω) juga dapat ditulis sebagai (s) untuk menunjukkan domain-S. dan fungsi transfer yang dihasilkan untuk low pass filter orde-2 kedua diberikan sebagai:

Polinomial Low Pass Filter Butterworth Normal

Untuk membantu dalam desain low pass filter-nya, Butterworth menghasilkan tabel standar dari normalisasi low pass orde-2 kedua polinomial yang diberi nilai koefisien yang sesuai dengan frekuensi sudut cut-off 1 radian/detik.

Desain Rangkaian Filter - Low Pass Butterworth

Temukan orde dari low pass filter aktif Butterworth yang spesifikasinya diberikan sebagai: Amax = 0,5dB pada frekuensi band pass ( ωp ) 200 radian/detik (31.8Hz), dan Amin = -20dB pada frekuensi band stop ( ωs ) dari 800 radian/detik. Juga merancang rangkaian filter Butterworth yang cocok untuk memenuhi persyaratan ini.

Pertama, band pass gain maksimum Amax = 0,5dB yang sama dengan gain 1.0593, ingat bahwa: 0,5dB = 20*log (A) pada frekuensi ( ωp ) 200 rad/s, sehingga nilai epsilon ε ditemukan oleh:

Kedua, stop band gain minimum Amin = -20dB yang sama dengan gain 10 (-20dB = 20*log(A)) pada frekuensi stop band ( ωs ) dari 800 rads/second atau 127,3Hz.

Mengganti nilai ke dalam persamaan umum untuk respon frekuensi filter Butterworth memberi kita yang berikut:

Karena n harus selalu berupa bilangan integer (bilangan bulat) maka nilai tertinggi berikutnya ke 2.42 adalah n = 3, oleh karena itu diperlukan “filter orde-3 ketiga” dan untuk menghasilkan filter Butterworth orde-3 ketiga, tahap filter orde-2 kedua diperlukan bersama-sama dengan tahap filter orde-1 pertama.

Dari tabel low pass Butterworth Polynomial yang dinormalisasi di atas, koefisien untuk filter orde-3 ketiga diberikan sebagai (1 + s) (1 + s + s2 ) dan ini memberi kita gain 3-A = 1, atau A = 2. Sebagai A = 1 + (Rf/R1), memilih nilai untuk kedua resistor umpan balik Rf dan resistor R1 memberi kita nilai 1kΩ dan 1kΩ masing-masing sebagai: ( 1kΩ/1kΩ) + 1 = 2.

Kita tahu bahwa frekuensi sudut cut-off, titik -3dB ( ωo ) dapat ditemukan menggunakan rumus 1/CR, tetapi kita perlu mencari ωo dari frekuensi band pass ωp kemudian,

Jadi, frekuensi sudut cut-off diberikan sebagai 284 rad/s atau 45.2Hz, (284/2π) dan menggunakan rumus akrab 1/CR kita dapat menemukan nilai-nilai resistor dan kapasitor untuk rangkaian orde-3 ketiga kita.

Perhatikan bahwa nilai pilihan terdekat ke 0,352uF adalah 0,36uF, atau 360nF.

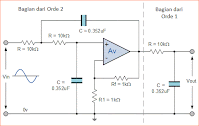
Low Pass Filter Butterworth Orde-3 ketiga

dan akhirnya rangkaian kita dari low pass Filter Butterworth orde-3 ketiga dengan frekuensi sudut cut-off 284 rads/s atau 45.2Hz, gain band pass maksimum 0.5dB dan gain stop band minimum 20dB dibuat sebagai berikut.

Jadi untuk Low Pass Filter Orde-3 ketiga kita dengan frekuensi sudut 45.2Hz, C = 360nF dan R = 10kΩ